6 

5   La détection par corrélation spectrale dans l’espace des vitesses

5.1  Principe

le principe de base de cette méthode est en fait assez simple. Considérons une étoile dont nous connaissons le spectre S_e(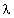). Supposons maintenant qu’autour de cette étoile, gravite une planète. Le flux lumineux que nous recevons de celle-ci provient essentiellement, dans le domaine allant de l’ultraviolet à l’infrarouge moyen, du flux incident venant de l’étoile diffusé par les composés atmosphériques ou réfléchi sur la surface avec un certain coefficient d’albédo. Le spectre issu de la planète et donc similaire à celui de l’étoile, mais atténué et décalé en longueur d’onde du fait du déplacement de la planète autour de l’étoile. On peut donc exprimer ce spectre S_p(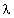) par :

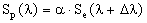(1)

ou

Le spectre total que nous mesurons sur l’ensemble étoile + planète est donc :

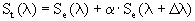(2)

où 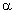est le rapport du flux réémis par la planète sur le flux de l’étoile. On peut également exprimer ce spectre non pas en fonction de la longueur d’onde, mais en fonction d’une vitesse fictive V définie en intégrant l’expression de 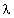. On obtient alors les expressions suivantes :

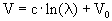(3)

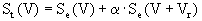(4)

Examinons maintenant la fonction d’autocorrélation d’énergie c_aa(x) d’une fonction réelle a. Celle ci a pour expression :

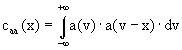(5)

Cette fonction présente un maximum en x = 0, ce qui se démontre facilement avec l’inégalité de Schwartz.. Calculons maintenant la fonction d’autocorrélation d’énergie de S_e et la fonction d’intercorrélation d’énergie de S_e et S_t :

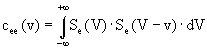(6)

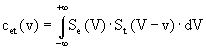(7)

L’équation (7) peut encore s’écrire en prenant en compte (4) et (6) :

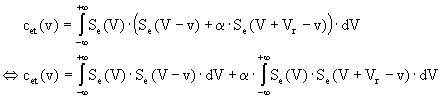
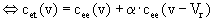(8)

On voit donc que la fonction d’intercorrélation d’énergie de S_e et S_t présente toujours un maximum en zéro, mais elle présente en plus un maximum secondaire en V_r.

A partir d’un certain nombre de spectres d’un couple étoile + planète, on peut obtenir, en les moyennant, un spectre proche du spectre de l’étoile seule, dit spectre de référence. En intercorrélant ce spectre de référence avec des spectres pris à des dates différentes, on doit observer sur les fonctions d’intercorrélation un maximum principal fixe en zéro et un maximum secondaire dont la position et l’amplitude varie en fonction de la vitesse de la planète suivant la direction d’observation, donc en fonction de la date. On effectue la corrélation dans l’espace des vitesse plutôt que dans l’espace des longueurs d’onde d’une part parce que cela permet d’obtenir directement la vitesse V_r, et d’autre part parce que cela évite la variation du décalage en fonction de la longueur d’onde.

Pour augmenter le contraste, on peut s’intéresser à c_et( v )-c_et( -v ). Notons C±( v ) cette expression. On a alors :

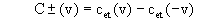
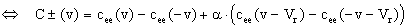(9)

Or la fonction d’autocorrélation d’énergie est symétrique. On a donc :

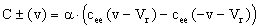(10)

Nous avons donc supprimé le maximum principal ainsi que tout ce qui était symétrique, et donc augmenté le contraste sur le maximum secondaire.

Maintenant que le principe de la méthode est connu, il nous est possible d’estimer les résultats qu’elle permettra d’obtenir sur les données concernant 51 Peg, qui est l’étoile sur laquelle nous avons travaillé.

[  Sommaire  |  Première  |  précédante  |  Acceuil   | suivante  |  Dernière  ]
[  1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17  ]
Laboratoire Interuniversitaire des Systèmes Atmosphériques
URA 1404 du CNRS - Université Paris XII - Val de Marne
This Manual was created with ManStyle.