13 

7   Analyse des résultats

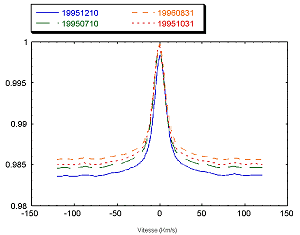
La Figure 10 représente les fonctions d’intercorrélation de 4 fichiers. On remarque la similitude avec la fonction d’autocorrélation du fichier de référence. Toutefois, on constate également que la normalisation ne fonctionne pas aussi bien que pour l’autocorrélation.

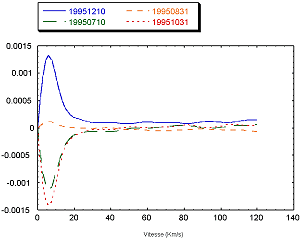
Intéressons nous maintenant à la fonction C±(v) définie dans le chapitre 5.1. Cette fonction est représentée pour quatre fichiers sur la Figure 11. On constate la présence d’un lobe proche de zéro. Celui-ci est du au fait que le maximum de la fonction d’intercorrélation n’est connu qu’à un point près. Lorsque l’on effectue la différence entre les vitesses positives et les vitesses négatives, le décentrage qui résulte de l’erreur commise sur le maximum génère ce lobe.

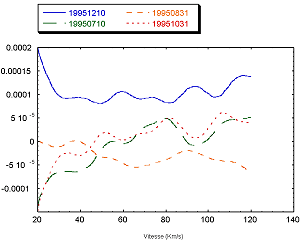
Examinons maintenant un grossissement de la partie plane. La Figure 12 représente ce zoom. On voit des ondulations dont l’amplitude empêche toute détection possible du maximum du à la planète. De plus, on remarque l’existence d’une pente qui varie suivant le fichier considéré. Dans un premier temps, nous n’avons pas trouvé d’explication à cette pente. Toutefois, elle est assez facile à déterminer et à corriger, ce que nous avons fait. Reste les oscillations. Elles peuvent elles aussi trouver leur justification dans l’incertitude concernant la position du maximum. Nous avons donc effectué un sur-échantillonnage de ces fonctions en interpolant avec un polynôme chaque groupe de quatre points de la fonction d’intercorrélation, ceci afin de pouvoir recaler celle-ci avec précision.

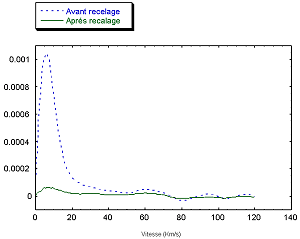
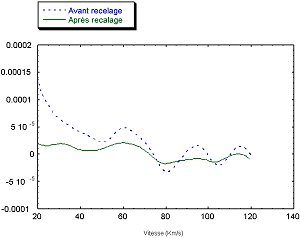
La Figure 13 montre le résultat du redressement et du recalage. Le lobe principal a été fortement atténué. Un zoom sur la partie plane est donné Figure 14. On constate que les ondulations ont bien été atténuées, mais elles existent toujours, et leur amplitude empêche toujours toutes possibilités de détecter le maximum du à la planète. Cette fois ci, les ondulations restantes ne sont pas dûes au mauvais recalage, mais semblent être dues à la nature même des spectres utilisés. d’où pouvait elles provenir ?

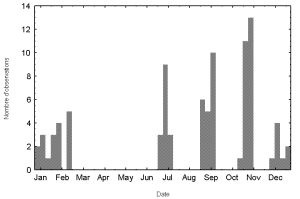
En examinant la liste des fichiers, fournie en annexe 3, on constate que les observations ne sont pas faites de manière uniforme sur toute l’année, mais sont au contraire regroupées par périodes. la Figure 15 représente la répartition des observations dans l’année. On remarque qu’elles sont regroupées en quatre périodes principales. La première va de début décembre à mis février, la deuxième de fin juin à mi juillet, la troisième de fin août à mi septembre, et enfin la quatrième de fin octobre à début novembre.

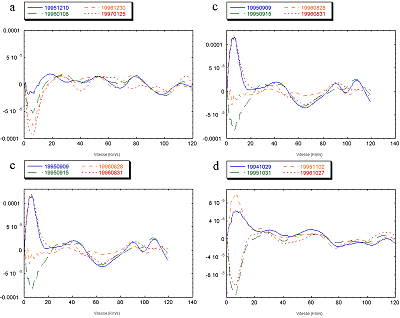
Regardons maintenant la fonction C±(v) pour des fichiers pris dans la même période de l’année. Ce regroupement est fait sur la Figure 16. On constate que les ondulations sont fortement semblabes au sein d’une même période. Ceci nous à permis d’utiliser un algorithme basé sur la prédiction de la position du maximum du à la planète.

Ce que nous cherchons à connaître, c’est la vitesse maximale du compagnon. Or nous connaissons sa période de révolution et sa phase (c.f. Tableau 1). L’algorithme consiste à éffectuer pour chaque période une moyenne des fonctions C±(v), moyenne que l’on soustrait aux différentes fonctions afin de diminuer les ondulations. Puis, on fait une prédiction de la position du maximum du à la planète pour chacun des fichiers et pour différentes valeurs de la vitesse maximale. On fait ensuite la somme des amplitudes des fonctions C±(v) à la position prédite. On représente ensuite ces sommes en fonction de la valeur de la vitesse maximale utilisée. Cette courbe doit présenter un maximum à l’endroit où la vitesse correspond effectivement à la vitesse du compagnon. En effet, si la prédiction ne concorde pas avec la position réelle du maximum, la somme des amplitudes doit osciller autour de zéro chaque fois que l’on ajoute un terme. Par contre, si la prédiction concorde, chaque fois que l’on ajoute un terme, la somme des amplitudes croit.

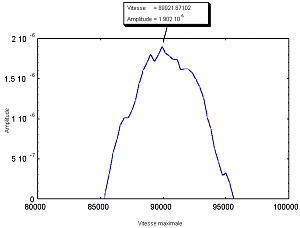
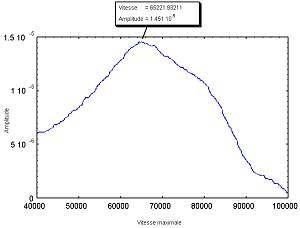
La principale limitation de cet algorithme est qu’il faut connaître avec une grande précision la période et la phase de la planète. Or, les données fournies par Mayor et celles fournies par Marcy diffèrent de façon très sensible. Nous avons appliqué cet algorithme avec ces deux jeux de données sur les fichiers de la troisième période. Les résultats sont donnés Figure 17 et Figure 18. Dans les deux cas, on peut déterminer une vitesse maximale, ce qui est impossible...

Figure 17: Utilisation des paramètres issus de Mayor et Queloz [13] pour déterminer l'amplitude maximale à l'aide de prédictions.

Figure 18: Utilisation des paramètres issus de Marcy et Butler [12] pour déterminer l'amplitude maximale à l'aide de prédictions.

Il apparaît donc que les ondulations ont un effet trop important pour permettre l’application de l’algorithme. Il nous fallait absolument en trouver l’origine. Mais le temps nous a manqué pour pouvoir les corriger.

[  Sommaire  |  Première  |  précédante  |  Acceuil   | suivante  |  Dernière  ]
[  1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17  ]
Laboratoire Interuniversitaire des Systèmes Atmosphériques
URA 1404 du CNRS - Université Paris XII - Val de Marne
This Manual was created with ManStyle.