9 



«Recherche directe de planètes extrasolaires par méthode de corrélation spectrale dans l'espace des vitesses»
 

6.2  Préparation des données.

6.2.1 Correction des pixels défectueux.

En examinant certains fichiers, nous nous sommes rendu compte que certains pixels présentaient des valeurs aberrantes, soit qu’ils étaient à zéro, soit qu’au contraire ils avaient une valeur beaucoup plus grande que celles des pixels voisins. Le guide de l’utilisateur du programme de réduction du spectrographe Elodie donne une liste des pixels défectueux répertoriés. Ceux-ci sont d’ailleurs pris en compte et corrigés lors de la réduction. Mais ceux que nous avions repérés ne faisaient pas partie de cette liste. Certains d’entre eux apparaissaient de manière systématique dans tous les fichiers, d’autres de manière épisodique.

Ces pixels défectueux peuvent être soit des pixels réellement endomagés, soit des pixels pour lesquels une erreur s’est produite lors du déchargement de la caméra CCD.

Nous avons donc mis au point un algorithme de correction des pixels défectueux. Il est basé sur la comparaison de l’écart entre la valeur du pixel et celle des pixels adjacents avec la valeur de l’écart type de cette écart sur les 100 pixels encadrant le pixel testé. Si cet écart est supérieur à 3 fois l’écart type, le pixel est considéré comme défectueux et sa valeur est recalculée en interpolant avec les valeurs des deux pixels adjacents.

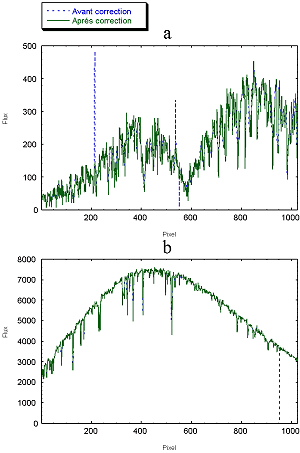
De plus, pour éviter que les raies de 51Peg ne soient identifiées comme des pixels défectueux, nous supposons qu’il ne peut y avoir plus de deux pixels défectueux consécutifs. Cet algorithme a donné de très bons résultats puisqu’il a permis de corriger une grande partie des pixels défectueux, notamment 69 pixels systématiquement défectueux. La Figure 4 présente le résultat pour les ordres 3 et 52 d’un des fichiers et l’annexe 2 donne la liste de ces 69 pixels.

 

Figure 4: Exemple de résultats de la correction des pixels défectueux sur a/ l'ordre 3 et b/ l'ordre 52 du fichier 19940916s2d0014. On voit clairement que lespixels 214, 535 et 551 de l'ordre 3 ont été corrigés, ainsi que le pixel 952 de l'ordre 52.

 

Une fois ces pixels corrigés, l’étape suivante du traitement a consisté en un rééchantillonnage des fichiers, que nous allons maintenant décrire.

6.2.2 Rééchantillonnage des données.

On peut se demander pourquoi ce rééchantillonnage. La première justification est que les fichiers S2D sont des fichiers donnant le flux pour une plage de longueur d’onde correspondant à un pixel, la longueur d’onde associée à un pixel n’étant qu’une longueur d’onde moyenne. Pour pouvoir les utiliser, il fallait les transformer de façon à ce qu’ils donnent une intensité au lieu du flux. De plus, les spectres n’avaient pas un pas en longueur d’onde constant. Or, pour pouvoir utiliser la fonction d’intercorrélation discrète, il faut que les deux tableaux de données utilisées aient le même pas. Il faut également qu’il y ai correspondance entre les ordonnées des deux tableaux, c’est à dire que chaque fichier utilise les mêmes séries de longueurs d’onde discrètes, ce qui n’était pas le cas dans les fichiers S2D. Ce rééchantillonnage a donc permis d’une part d’avoir un fichier en intensité, d’autre part d’avoir un pas constant et de recaler les fichiers entre eux. De plus nous avons profiter de ce rééchantillonnage pour exprimer les spectres non pas en fonction de la longueur d’onde mais d’une vitesse fictive, telle qu’elle a été définie dans le chapitre 5.1.

Pour effectuer le rééchantillonnage, nous voulions conserver le flux pour chaque pixel, ceci afin de ne pas perdre d’information. Pour ce faire, nous avons approché l’intensité pour chaque pixel par un polynôme de degré 3. Une approximation par une fonction de degré inférieur n’était pas envisageable car cela générait une divergence très rapide du calcul due à un phénomène d’oscillation de très forte amplitude. L’utilisation d’un degré 3 ne fait pas disparaître les oscillations mais permet de les contraindre.

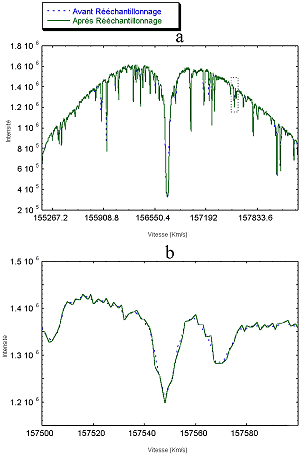
La Figure 5 montre le résultat du rééchantillonage sur l’ordre 64 d’un des fichiers. Le fichier rééchantillonné est ici comparé avec un fichier obtenu en divisant la valeur de chaque pixel par la largeur de celui-ci en longueur d’onde. Nous pouvons voir des oscillations dont la période est de l’ordre du pixel initial. A priori, ces oscillations ne devaient pas gêner la suite du traitement.

 

Figure 5: Résultat du rééchantillonnage sur l'ordre 64 du fichier 1994s2d0017. A l'echelle de l'ordre, la correspodance entre les fichiers est trés bonne (a), mais un zoom sur une petite partie de l'ordre (b) fait apparaître des oscillations autour des valeurs d'origines.

 

Une fois tous les fichiers rééchantillonnés, nous somme passé à la génération du fichier de moyen nécessaire au calcul de l’intercorrélation.


[  Sommaire  |  Première  |  précédante  |  Acceuil   | suivante  |  Dernière  ]
[  1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17  ]
Laboratoire Interuniversitaire des Systèmes Atmosphériques
URA 1404 du CNRS - Université Paris XII - Val de Marne
This Manual was created with ManStyle.