7
|
«Recherche directe de planètes extrasolaires par méthode de corrélation spectrale dans l'espace des vitesses» |
51 Peg est une étoile similaire au soleil. Elle est de type spectrale G2Iva et se trouve actuellement dans la séquence principale. Elle se situe à environ 50 années lumière du soleil. Le Tableau 3 rapporte ses caractéristiques principales en comparaison de celles du soleil.
| Soleil | 51 Pegasi | |
| Masse / M | 1.00 | 0.95 |
| Rayon / R | 1.00 | 1.3 - 1.4 |
| Température de surface | 5780 K | ~ 5700 K |
| Métallicité / Met | 1.00 | 1.2 - 1.5 |
| Magnitude apparente | 5.49 |
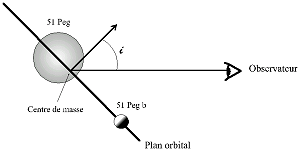
En octobre 1995, Michel Mator et Didier Queloz, de l’Observatoire de Genève, ont annoncé la découverte d’un compagnon à cette étoile [13], découverte confirmée par Geoffrey W. Marcy et R. Paul Butler [12]. Les deux corps gravitant autour de leur centre de masse, il en résulte une variation de leur vitesse radiale, c’est à dire de leur vitesse projetée sur la ligne de visée. La Figure 1 montre la configuration dans laquelle on observe l’étoile et son compagon. Les mesures de la vitesse radiale de 51 Peg ont été effectuées avec le spectromètre Elodie, instrument installé sur le télescope de 1,93 m de l’Observatoire de Haute Provence.
|
|
|
|
Ces mesures ont mis en évidence des variations périodiques de cette vitesse, d’une période de 4,23 jours, avec une amplitude de 59 m/s. Comme nous l’avons déjà dit, on ne mesure que la vitesse de l’étoile au sinus de l’inclinaison i près. De ce fait, on ne peut connaître la masse du compagnon qu’à ce même sinus près. Les caractéristiques du compagnon qui provoque ces variations sont données dans le Tableau 4. On peut voir que suivant la source, ces données varient de façon sensible, ce qui posera par la suite quelques problèmes.
|
| |
| Vitesse maximale de l'étoile | 59 m.s-1 | 55.9 ±0.8 m.s-1 |
| Période de révolution |
|
|
| Phase |
|
|
| M.Sin( i ) / Mj | 0.47 ±0.02 | 0.45 |
| Excentricité | ~0 | 0.012 ±0.01 |
| Demi grand axe | 0.05 | 0.051 |
Nous allons maintenant estimer l’amplitude de l’écho que nous recherchons. Cette estimation est en effet nécessaire pour d’une part avoir une idée de ce que l’on recherche, et d’autre part pour obtenir, une fois que l’amplitude aura été mesurée, une estimation de la taille de la planète.
Pour estimer l’amplitude de l’écho, il nous faut d’abord connaître l’albédo géométrique 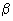 de 51 Peg b. Ne connaissant pas la composition de 51 Peg b, nous avons pris pour celui-ci un valeur moyenne de
de 51 Peg b. Ne connaissant pas la composition de 51 Peg b, nous avons pris pour celui-ci un valeur moyenne de 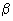 = 0.5. Il nous faut également rendre compte de la phase de la planète. nous utilisons pour cela un paramètre
= 0.5. Il nous faut également rendre compte de la phase de la planète. nous utilisons pour cela un paramètre 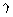 compris entre 0 et 1.
compris entre 0 et 1.
|
|
|
|
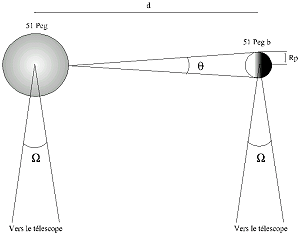
Considérons maintenant la Figure 2. Soit  l’angle solide sous lequel est vu le compagnon depuis l’étoile centrale. La fraction du flux émis par l’étoile qui est reçu par la planète est de
l’angle solide sous lequel est vu le compagnon depuis l’étoile centrale. La fraction du flux émis par l’étoile qui est reçu par la planète est de  /4
/4 . Ce flux n’est ré-émis que sur 2
. Ce flux n’est ré-émis que sur 2 . Soit maintenant
. Soit maintenant 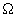 l’angle solide sous lequel est vu le télescope depuis le système 51 Peg / 51 Peg b. Si on note Ft le flux total émis par l’étoile, le flux Fp que le télescope reçoit de la planète est donc de :
l’angle solide sous lequel est vu le télescope depuis le système 51 Peg / 51 Peg b. Si on note Ft le flux total émis par l’étoile, le flux Fp que le télescope reçoit de la planète est donc de :
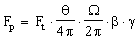 (11)
(11)
De même le flux Fe qu’il reçoit de l’étoile est de :
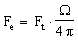 (12)
(12)
Le rapport du flux ré-émis par la planète sur le flux de l’étoile 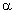 est donc de :
est donc de :
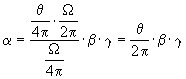 (13)
(13)
L’angle solide  peut s’exprimer en fonction du rayon Rp de 51 Peg b et de sa distance à l’étoile d par :
peut s’exprimer en fonction du rayon Rp de 51 Peg b et de sa distance à l’étoile d par :
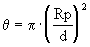 (14)
(14)
d’ou finalement :
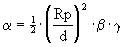 (15)
(15)
A présent, nous allons voir comment, à partir des informations déjà connues sur 51 Peg b et de celles que fournira la méthode de corrélation spectrale, on peut préciser les paramètres du couple 51 Peg / 51 Peg b.
Si on note Vremax la vitesse radiale maximale de l’étoile et Vrpmax la vitesse radiale maximale du compagnon, nous pouvons exprimer ces deux vitesses en fonction des masses des deux corps, de la distance les séparant, de l’inclinaison de leur orbite par rapport à la direction d’observation et de la constante de gravitation. nous avons alors les expressions suivantes :
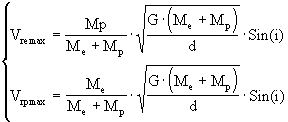 (16)
(16)
ou 
En effectuant le rapport de Vremax sur Vrpmax , nous avons :
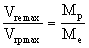 (17)
(17)
Connaissant la masse de 51 Peg, nous pouvons donc en déduire celle de son compagnon. Notons Ms la masse du soleil et MJ la masse de Jupiter. Nous avons alors :
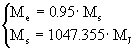
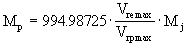 (18)
(18)
Connaissant Mp.Sin(i), nous pouvons dès lors calculer l’inclinaison de l’orbite par rapport à la direction d’observation.
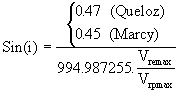 (19)
(19)
Enfin, une fois que nous aurons l’amplitude des piques secondaires sur la fonction C±(v), il nous sera possible à partir de (15) et de (10), en supposant que la valeur de l’albédo géométrique 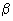 est exacte, d’estimer le rayon de la planète.
est exacte, d’estimer le rayon de la planète.
Maintenant que la théorie est en place, nous allons nous intéresser à la mise en pratique de la méthode sur les données issues d’Elodie.